统计学习方法第五章—决策树

1.决策树模型与学习

1.1 决策树模型

内部节点代表一个特征或属性，叶结点代表一个类。

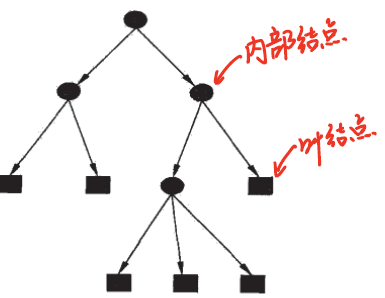
1.2 决策树与if-then规则

可将决策树看成一个if-then规则的集合，重要性质：互斥且完备，每一个实例有且只被一条路径或规则覆盖。

1.2 决策树与条件概率分布

决策树还表示给定特征条件下类的条件概率分布。这一条件概率分布定义在特征空间的一个划分上。决策树的一条路径对应于划分中的一个单元。

1.3 决策树学习

找到与训练数据矛盾较小且泛化能力好的决策树。损失函数：正则化的极大似然函数。

主要步骤：

• 特征选择
• 决策树生成
• 决策树剪枝

2.特征选择

准则：信息增益/信息增益比 ### 2.1 信息增益 熵：随机变量不确定程度。

设X为取有限个值的随机变量，概率分布为：\(P\left(X=x_{i}\right)=p_{i}, \quad i=1,2, \cdots, n\) 随机变量X的熵：\(H(X)=H(p)=-\sum_{i=1}^{n} p_{i} \log p_{i}\) \(H(p)\)满足\(0 \leqslant H(p) \leqslant \log n\)

条件熵\(H(Y|X)\)：已知随机变量X的条件下随机变量Y的不确定性，定义为X给定条件下Y的条件概率分布的熵对X的数学期望 \[ H(Y | X)=\sum_{i=1}^{n} p_{i} H\left(Y | X=x_{i}\right) \\ p_i=P(X=x_i),i=1,2,\cdots,n \]

熵和条件熵中的概率由数据估计（特别是极大似然估计）得到，分别称为经验熵和经验条件熵。

信息增益g(D,A)：特征A对训练集D信息增益为D的经验熵H(D)与特征A给定条件下D的经验条件熵H(D|A)之差： \[ g(D, A)=H(D)-H(D | A) \]

根据信息增益的特征选择方法：对训练集（或子集）D，计算其各个特征的信息增益，选择信息增益最大的特征。

2.2 信息增益比

信息增益比：特征A对训练集D信息增益比为其信息增益g(D,A)与D的经验熵H(D)之比： \[ g_{R}(D, A)=\frac{g(D, A)}{H(D)} \]

3.决策树的生成

3.1 ID3算法

在决策树各个结点上应用信息增益准则选择特征，递归地构建决策树。ID3相当于用极大似然法进行概率模型的选择。 ### 3.2 C4.5算法 过程与ID3算法相似，不同的是用信息增益比来选择特征。

4.决策树的剪枝

过程：从已生成的树上裁掉一些子树或叶结点，并将其根结点或父结点作为新的叶结点，从而简化分类树模型，极小化决策树整体的损失函数。

决策树学习的损失函数：\(C_{\alpha}(T)=\sum_{t=1}^{|T|} N_{t} H_{t}(T)+\alpha|T|\) 其中经验熵：\(H_{t}(T)=-\sum_{k} \frac{N_{tk}}{N_{t}} \log \frac{N_{t k}}{N_{t}}\) 将损失函数右端第一项记作：\(C(T)==-\sum_{t=1}^{|T|} \sum_{k=1}^{K} N_{t k} \log \frac{N_{t k}}{N_{t}}\)

此时有：\(C_{\alpha}(T)=C(T)+\alpha|T|\)

C(T)表示模型对训练数据的预测误差，即模型与训练数据的拟合程度，|T|表示模型复杂度，参数 \(\alpha\geq0\) 控制两者之间的影响。较大的 \(\alpha\) 促使选择较简单的模型。

5.CART算法

分类与回归树 - 回归树：平方误差最小化准则 - 分类树：基尼指数最小化准则

5.1 分类树生成

（1）概率分布的基尼指数：\(\operatorname{Gini}(p)=\sum_{k=1}^{K} p_{k}\left(1-p_{k}\right)=1-\sum_{k=1}^{K} p_{k}^{2}\) 对于二类问题：\(\operatorname{Gini}(p)=2p(1-p)\) 给定样本集合D的基尼指数：\(\operatorname{Gini}(D)=1-\sum_{k=1}^{K}\left(\frac{\left|C_{k}\right|}{|D|}\right)^{2}\)，\(C_k\)为属于第k类的样本子集。

若样本集合D根据某一可能值a被分成\(D_1\)和\(D_2\)两部分，在特征A条件下，集合D的基尼指数为 \[\operatorname{Gini}(D, A)=\frac{\left|D_{1}\right|}{|D|} \operatorname{Gini}\left(D_{1}\right)+\frac{\left|D_{2}\right|}{|D|} \operatorname{Gini}\left(D_{2}\right)\]

基尼指数Gini(D)表示集合D的不确定性，基尼指数Gini(D,A)表示经A=a分割后集合D的不确定性。基尼指数值越大，样本集合的不确定性也就越大。

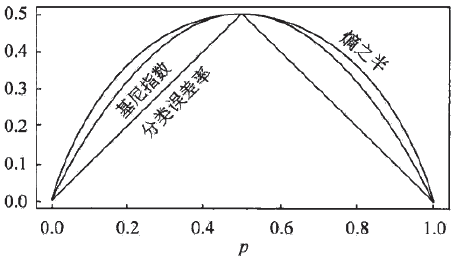
5.2 CART剪枝

（1）首先从生成算法产生的决策树\(T_0\)底端开始不断剪枝，直到\(T_0\)的根结点，形成一个子树序列\(\left\{T_{0}, T_{1}, \cdots, T_{n}\right\}\) （2）然后通过交叉验证法在独立的验证数据集上对子树序列进行测试，从中选择最优子树.