统计学习方法第二章—感知机

感知机——二类分类的线性分类模型

1.感知机模型

输入空间（特征空间）为 \(\mathcal{X}\subseteq R^n\)，输出空间为 \(\mathcal{Y}\subseteq \{+1,-1\}\)，输入 \(x\in\mathcal{X}\) 表示实例的特征向量，输出 \(y\in\mathcal{Y}\) 表示实例的类别，输入到输出空间的函数： \(f(x)=\operatorname{sign}(w \cdot x+b)\) 称为感知机，其中w:权值，b:偏置

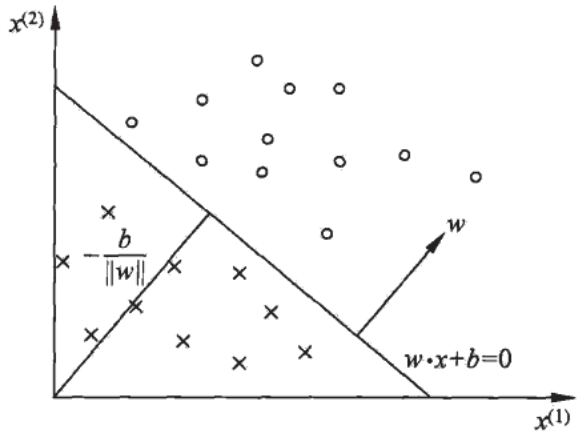
感知机几何解释：线性方程 \(w\cdot x+b=0\) 对应于特征空间\(R^n\)中的一个超平面S，w为超平面的法向量，b为超平面的截距，S将特征空间分为两个部分，位于两部分的点分别被分为正、负两类。

2.感知机学习策略

2.1 数据集的线性可分性

存在某个超平面S可将数据集的正实例点和负实例点完全正确地划分到S两侧即为线性可分。

2.2 学习策略

输入空间 \(R^n\) 中任一点 \(x_0\) 到超平面S的距离：\(\frac{1}{\|w\|}\left|w \cdot x_{0}+b\right|\)

误分类点 \(x_i\)到超平面S的距离：\(-\frac{1}{\|w\|} y_{i}\left(w \cdot x_{i}+b\right)\)

所有误分类点到超平面S的总距离：\(-\frac{1}{\|w\|} \sum_{x_{i}\in M} y_{i}\left(w \cdot x_{i}+b\right)\)

不考虑\(\frac{1}{\|w\|}\)即得到了感知机学习的损失函数（经验风险）：

\(L(w, b)=-\sum_{x_{i} \in M} y_{i}\left(w \cdot x_{i}+b\right) \quad\) (M：误分类点集合)

3.感知机学习算法

3.1学习算法原始形式

随机梯度下降法： 任选一个初始超平面\(w_0、b_0\)，每次选择一个误分类点 \(y_{i}\left(w \cdot x_{i}+b\right) \leqslant 0\) 使其梯度下降。 \(w \leftarrow w+\eta y_{i} x_{i}\) \(b \leftarrow b+\eta y_{i}\)

3.2学习算法对偶形式

通过\(w \leftarrow w+\eta y_{i} x_{i}\)，\(b \leftarrow b+\eta y_{i}\)逐步修改w,b，设修改n次，则w,b关于\((x_i,y_i)\)的增量为\(\alpha_iy_ix_i\)和\(\alpha_iy_i\)，其中\(\alpha_i=n_i\eta\)，最终学到的w,b可表示为 \(w=\sum_{i=1}^{N} \alpha_{i} y_{i} x_{i}\) \(b=\sum_{i=1}^{N} \alpha_{i} y_{i}\)

取初值\(\alpha \leftarrow 0, \quad b \leftarrow 0\)，训练集中选取数据\(\left(x_{i}, y_{i}\right)\)，如果\(y_{i}\left(\sum_{j=1}^{N} \alpha_{j} y_{j} x_{j} \cdot x_{i}+b\right) \leqslant 0\) 则 \(\alpha_{i} \leftarrow \alpha_{i}+\eta\)，\(b \leftarrow b+\eta y_{i}\)