复合材料失效准则
1.概述
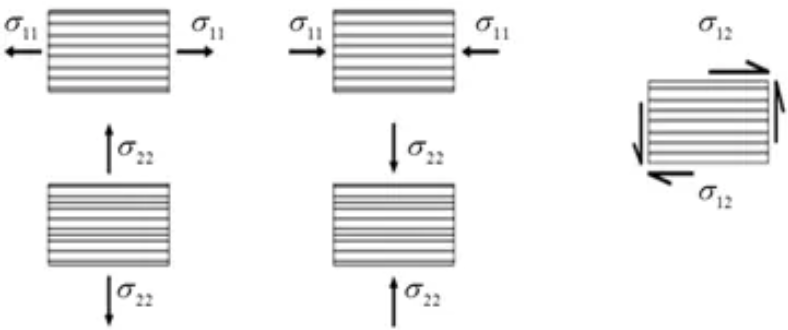
单个铺层一般的应力状态有以下某种或者是几种的组合:
- 沿纤维方向的拉伸应力,对应纤维拉断或者纤维拔出失效模式
- 沿纤维方向的压缩应力,对应纤维的局部失稳、纤维扭结等失效
- 沿垂直于纤维方向的拉伸,对应基体拉断
- 沿垂直于纤维方向的压缩应力,对应基体剪切失效
- 剪切应力,对应宏观剪切失效
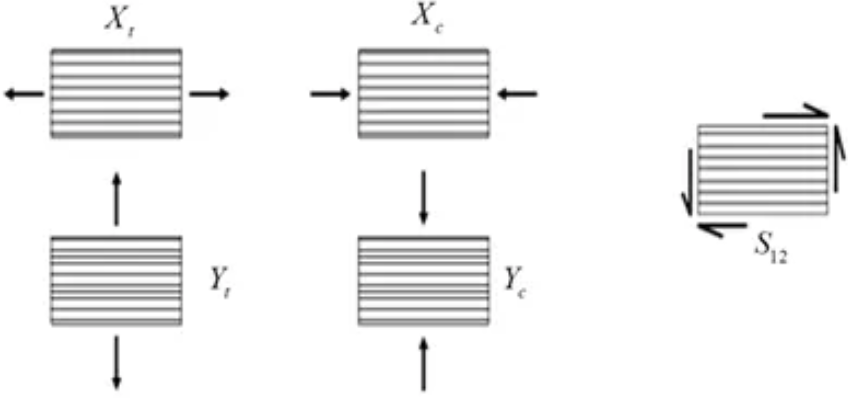
进行失效评估时,上述几种单一应力状态,都有相应的材料强度数值,下图所示即为层压板面内的强度数值 \(X_t\)、\(X_c\)、\(Y_t\)、\(Y_c\)、\(S_{12}\) ,与 4 个工程弹性常数(\(E_1\)、\(E_2\)、\(G_{12}\)、\(\nu_{12}\))一起,称为复合材料的 9 个工程常数。
\(X_t\):纵向拉伸强度
\(X_c\):纵向压缩强度
\(Y_t\):横向拉伸强度
\(Y_c\):横向压缩强度
\(S_{12}\):面内剪切强度
2.经典复合材料失效准则
2.1 最大应力准则
材料主方向上的应力必须小于各自方向上对应的强度,否则即发生破坏,这里的主方向指沿纤维方向和垂直纤维方向。
\[\begin{array}{lll} \sigma_{1}>X_{c} & \sigma_{2}>Y_{c} & \left|\tau_{12}\right|<\mathbf{S} & \text { 压缩时 } \\ \sigma_{1}<X_{t} & \sigma_{2}<Y_{t} & \left|\tau_{12}\right|<\mathbf{S} & \text { 拉伸时 } \end{array}\]
2.2 最大应变准则
单层板在平面应力状态下,主方向的任意一个分量达到极限应变时,就发生破坏或失效。
\[\begin{aligned} &\varepsilon_{1}<X_{\varepsilon_{1}} \quad \varepsilon_{2}<Y_{\varepsilon_{1}}\quad \left|\gamma_{12}\right|<S_{\varepsilon} \quad \text { 拉伸时 }\\ &\varepsilon_{1}>X_{\varepsilon_{0}} \quad \varepsilon_{2}>Y_{\varepsilon_{0}} \quad \left|\tau_{12}\right|<S_{\varepsilon} \quad \text { 压缩时 } \end{aligned}\]
2.3 Tsai-Hill 准则
进一步提高各向应力关系之间的阶数,就得到了二阶近似模型,其中,Tsai-Hill 理论是最早期的代表之一,Tsai-Hill 理论仅有一个表征失效的变量,无法区分具体的失效模式,另外该理论没有区分拉压强度的不同。
\[\frac{\sigma_{1}^{2}}{X^{2}}-\frac{\sigma_{1} \sigma_{2}}{X^{2}}+\frac{\sigma_{2}^{2}}{Y^{2}}+\frac{\tau_{12}^{2}}{S^{2}}=1\]
2.4 Hoffman 准则
Hoffman 准则在 Tsai-Hill 准则的基础上,考虑了材料在同一方向上的拉伸和压缩强度的不同。
\[\frac{\sigma_{1}^{2}-\sigma_{1} \sigma_{2}}{X_{t} X_{c}}+\frac{\sigma_{2}^{2}}{Y_{t} Y_{c}}+\frac{X_{c}-X_{t}}{X_{t} X_{c}} \sigma_{1}+\frac{Y_{C}-Y_{t}}{Y_{t} Y_{c}} \sigma_{2}+\frac{\tau_{12}^{2}}{S^{2}}=1\]
2.5 Tsai-Wu 准则
鉴于 Tsai-Hill 理论和 Hoffman 理论中缺乏 \(\frac{\sigma_1\sigma_2}{X_cX_t}\) 或 \(\frac{\sigma_1\sigma_2}{Y_cY_t}\) 项的影响,蔡为伦和 EdwardM.Wu 于 1971 年提出了新的张量理论,假定在应力空间内,破坏表面可以表示为一个二次张量多项式形式:
\[F_{1} \sigma_{1}+F_{2} \sigma_{2}+{F}_{6} \sigma_{6}+{F}_{11} \sigma_{1}^{2}+{F}_{22} \sigma_{2}^{2}+{F}_{66} \sigma_{6}^{2}+2 {F}_{12} \sigma_{1} \sigma_{2}={1}\]
其中:
\[\begin{array}{l} F_{1}=\frac{1}{X_{t}}+\frac{1}{X_{c}}, \quad F_{2}=\frac{1}{Y_{t}}+\frac{1}{Y_{c}}, \quad F_{11}=-\frac{1}{X_{t} X_{c}}, \quad F_{22}=-\frac{1}{Y_{t} Y_{c}}, \quad F_{66}=\frac{1}{S^{2}} \\ F_{12}=\frac{1}{2 \sigma_{\text {biax}}^{2}}\left[1-\left(\frac{1}{X_{t}}+\frac{1}{X_{c}}+\frac{1}{Y_{t}}+\frac{1}{Y_{c}}\right) \sigma_{\text {biax}}+\left(\frac{1}{X_{t} X_{c}}+\frac{1}{Y_{t} Y_{c}}\right) \sigma_{\text {biax}}^{2}\right] \end{array}\]
\(\sigma_{\text {biax}}\) 由双轴拉伸试验测得。
2.6 Hashin 准则
同样的二阶近似模型还有 Hashin 准则。Hashin 在 1980 年提出了一种三维的复合材料失效判据,该准则后被收录于 MILHDBK-17,在工程界与学术界应用甚广,目前其简化形式的二维失效判据已被集成在了 Abaqus、MSC.Dytran 等有限元软件中。
其简化后的三维表达形式如下:
- 纤维拉伸模式(\(\sigma_{11}\ge0\)):
\[\frac{\sigma_{11}^{2}}{X_{T}^{2}}+\alpha\left(\frac{\sigma_{12}^{2}+\sigma_{13}^{2}}{S_{12}^{2}}\right)=1\]
- 纤维压缩模式(\(\sigma_{11}<0\)):
\[\left(\frac{\sigma_{11}}{X_{c}}\right)^{2}=1\]
- 基体拉伸模式(\(\sigma_{22}+\sigma_{33}>0\)):
\[\frac{\left(\sigma_{22}+\sigma_{33}\right)^{2}}{Y_{T}^{2}}+\frac{\sigma_{12}^{2}+\sigma_{13}^{2}}{S_{12}^{2}}+\frac{\sigma_{23}^{2}-\sigma_{22} \sigma_{33}}{S_{23}^{2}}=1\]
- 基体压缩模式(\(\sigma_{22}+\sigma_{33}<0\)):
\[\left[\left(\frac{Y_{C}}{2 S_{23}}\right)^{2}-1\right] \frac{\sigma_{22}+\sigma_{33}}{Y_{C}}+\left(\frac{\sigma_{22}+\sigma_{33}}{2 S_{23}}\right)^{2}+\frac{\sigma_{23}^{2}-\sigma_{22} \sigma_{33}}{S_{23}^{2}}+\frac{\sigma_{12}^{2}+\sigma_{13}^{2}}{S_{12}^{2}}=1\]
Hashin 三维失效判据可以预测四种失效模式:纤维拉伸失效、纤维压缩失效、基体拉伸失效以及基体压缩失效等。在纤维拉伸失效中,考虑了剪切效应的影响。
Abaqus 中采用的是 2D 的 Hashin 准则,其表达形式如下:
- 纤维拉伸模式(\(\sigma_{11}\ge0\)):
\[\frac{\sigma_{11}^{2}}{X_{T}^{2}}+\alpha\left(\frac{\sigma_{12}^{2}}{S_{12}^{2}}\right)=\left\{\begin{array}{cc} \geq 1 & \text { failure } \\ <1 & \text { nofailure } \end{array}\right.\]
- 纤维压缩模式(\(\sigma_{11}<0\)):
\[\left(\frac{\sigma_{11}}{X_{c}}\right)^{2}=\left\{\begin{array}{ll} \geq 1 & \text { failure } \\ <1 & \text { nofailure } \end{array}\right.\]
- 基体拉伸模式(\(\sigma_{22}>0\)):
\[\left(\frac{\sigma_{22}}{Y_{T}}\right)^{2}+\frac{\sigma_{12}^{2}}{S_{12}^{2}}=\left\{\begin{array}{cc} \geq 1 & \text { failure } \\ <1 & \text { nofailure } \end{array}\right.\]
- 基体压缩模式(\(\sigma_{22}<0\)):
\[\left[\left(\frac{Y_{C}}{2 S_{23}}\right)^{2}-1\right] \frac{\sigma_{22}}{Y_{C}}+\left(\frac{\sigma_{22}}{2 S_{23}}\right)^{2}+\frac{\sigma_{12}^{2}}{S_{12}^{2}}=\left\{\begin{array}{cc} \geq 1 & \text { failure } \\ <1 & \text { nofailure } \end{array}\right.\]
上面看到的 Hashin 基体失效准则是简化后的公式,Hashin 准则最初的表达形式中,强度数值是断裂面上的强度,应力也是断裂面上的应力,与现在的 Puck 类似。
2.7 Chang-Chang失效准则
前面的准则中都是没有考虑材料的非线性的,层压板在 \(G_{12}\) 和 \(G_{13}\) 两个剪切方向是存在严重的剪切非线性的,考虑材料的剪切非线性行为,Chang 等把 Tsai-Hahn 的剪切非线性模型(一种表征层压板剪切非线性本构的力学模型)引入到失效准则中,提出了 Chang-Chang失效准则;Chang-Chang 失效判据被广泛应用于复合材料碰撞冲击等问题,目前三维 Chang-Chang 失效判据被集成于商业有限元软件 LS_DYNA 及 MSC.Dytran 中。
- 纤维压缩模式(\(\sigma_{11}<0\)):
\[\left(\frac{\sigma_{11}}{X_{T}}\right)^{2}+T=1\]
- 基体拉伸模式(\(\sigma_{22}\ge0\)):
\[\left(\frac{\sigma_{22}}{Y_{T}}\right)^{2}+T=1\]
- 基体压缩模式(\(\sigma_{22}<0\)):
\[\left(\frac{\sigma_{22}}{2 \mathrm{S}}\right)^{2}+\left[\left(\frac{\mathrm{Y}_{\mathrm{C}}}{2 \mathrm{S}}\right)^{2}-1\right] \frac{\sigma_{22}}{\mathrm{Y}_{\mathrm{C}}}+\mathrm{T}=1\]
其中, \[\mathrm{T}=\left(\frac{\sigma_{12}}{\mathrm{S}}\right)^{2} \frac{1+\frac{3}{2} \alpha \mathrm{G}_{12} \sigma_{12}^{2}}{1+\frac{3}{2} \alpha \mathrm{G}_{12} \mathrm{S}^{2}}\]
3.Hashin复合材料渐进失效模型原理及参数详解
3.1 二维应力应变关系
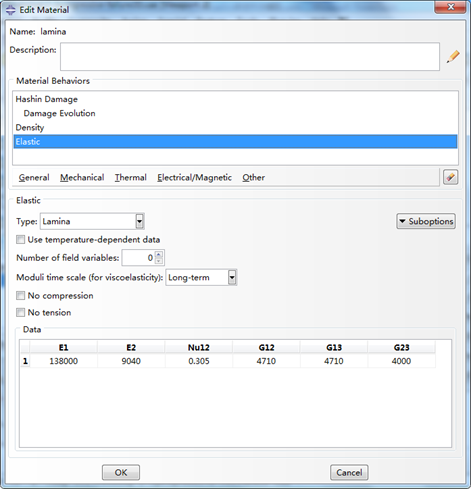
在 Abaqus 中 Hashin 失效准则适用于常规壳单元或者连续壳单元,对应的材料模型为 Lamina,应力应变关系如下:
\[\left\{\begin{array}{c} \varepsilon_{1} \\ \varepsilon_{2} \\ \gamma_{12} \end{array}\right\}=\left[\begin{array}{ccc} 1 / E_{1} & -\nu_{12} / E_{1} & 0 \\ -\nu_{12} / E_{1} & 1 / E_{2} & 0 \\ 0 & 0 & 1 / G_{12} \end{array}\right]\left\{\begin{array}{l} \sigma_{11} \\ \sigma_{22} \\ \tau_{12} \end{array}\right\}\]
其中,各参数满足稳定性约束条件:
\[\begin{array}{l} E_{1}, E_{2}, G_{12}, G_{13}, G_{23}>0 \\ \left|\nu_{12}\right|<\left(E_{1} / E_{2}\right)^{1 / 2} \end{array}\]
写成刚度矩阵的表达式如下:
\[\left\{\begin{array}{c} \sigma_{11} \\ \sigma_{22} \\ \tau_{12} \end{array}\right\}=\left[\begin{array}{ccc} E_{1} & v_{21} E_{1} & 0 \\ 1-v_{12} v_{21} & 1-v_{12} v_{21} & \\ \frac{v_{12} E_{2}}{1-v_{12} v_{21}} & \frac{E_{2}}{1-v_{12} v_{21}} & 0 \\ 0 & 0 & G_{12} \end{array}\right]\left\{\begin{array}{l} \varepsilon_{11} \\ \varepsilon_{22} \\ \gamma_{12} \end{array}\right\}\]
简写为:\(\boldsymbol{\sigma}=\boldsymbol{C}_{\mathbf{0}} \boldsymbol{\varepsilon}\),其中,\(\boldsymbol{C}_{\mathbf{0}}\) 为无损状态下的弹性矩阵。
欲表征材料的应力应变关系,在CAE中仅需要输入弹性常数即可。
3.2 二维Hashin准则表达式
在 Abaqus 中引入的二维的 Hashin 失效准则,共分为纵向拉伸(纤维方向拉伸)、纵向压缩(纤维方向压缩)、横向拉伸(垂直纤维方向拉伸)、横向压缩(垂直纤维方向压缩)等四种失效模式。

上述四个公式用于判断的是材料点的损伤起始,当 \(F_{ft}\) 达到 1 的时候,表示该材料点纤维方向拉伸损伤刚刚开始,小于 1 的时候,材料纤维方向无拉伸损伤。其他同理。绝大部分论文仅引用了这四个公式就去做渐进失效分析了,是不完整的,这仅仅能预测损伤的起始,还缺乏损伤起始以后的刚度退化。
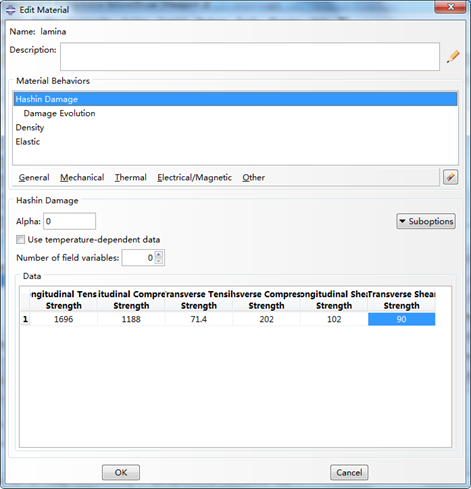
与损伤起始相关的是 6 个强度值,定义如下,6个参数分别是:纵向拉伸强度 \(X_T\),纵向压缩强度 \(X_C\),横向拉伸强度 \(Y_T\),横向压缩强度 \(Y_C\),纵向剪切强度 \(S_L\),横向剪切强度 \(S_T\)。
3.3 基于能量的损伤演化
定义损伤演化参数的界面如下,输入四种失效模式对应的断裂能:纵向拉伸断裂能 \(G_{ftc}\),纵向压缩断裂能 \(G_{fcc}\),横向拉伸断裂能 \(G_{mtc}\),横向压缩断裂能 \(G_{mcc}\)。(断裂能,即临界应变能释放率,是裂纹扩展单位面积所需要的能量,一般单位取为N/m,J/m²,N/mm或mJ/mm²。
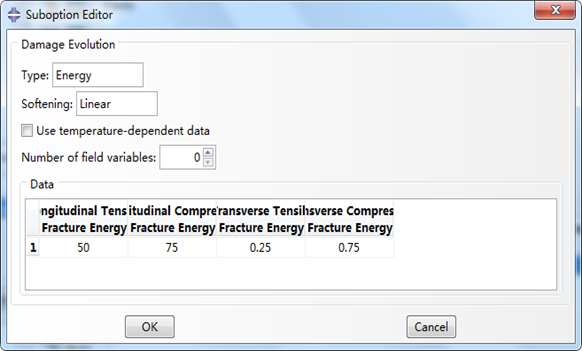
3.4 损伤状态变量的求解
损伤起始以后,材料的刚度将会发生逐渐退化,此时开始进入损伤演化阶段,材料的刚度退化程度用损伤状态变量 d 来表示。
含损伤的材料应力应变关系为:
\[\sigma=C(d) \varepsilon\]
其中:
\[\boldsymbol{C}(d)=\frac{1}{D}\left[\begin{array}{ccc} \left(1-d_{f}\right) E_{1} & \left(1-d_{f}\right)\left(1-d_{m}\right) v_{21} E_{1} & 0 \\ \left(1-d_{f}\right)\left(1-d_{m}\right) v_{12} E_{2} & \left(1-d_{m}\right) E_{2} & 0 \\ 0 & 0 & D\left(1-d_{s}\right) G \end{array}\right]\]
\[D=1-\left(1-d_{f}\right)\left(1-d_{m}\right) v_{12} v_{21}>0 ; \quad d_{s}=1-\left(1-d_{f t}\right)\left(1-d_{f c}\right)\left(1-d_{m t}\right)\left(1-d_{m c}\right)\]
上述公式中,
\(d_f\):纤维方向损伤状态变量
\(d_m\):基体方向损伤状态变量
\(d_s\):剪切损伤状态变量
\(d_f\),\(d_m\),\(d_s\) 的表达式是子的:
即纤维方向的损伤取决于纤维方向拉伸损伤状态 \(d_{ft}\) 和纤维方向压缩损伤状态 \(d_{fc}\),二者只能发生其中的一种,具体发生哪种由沿纤维方向的应力 \(\sigma_{11}\) 决定,当 \(\sigma_{11}\ge0\) 时,潜在发生的是纤维方向的拉伸损伤,取 \(d_f=d_{ft}\),反之,发生纤维方向的压缩损伤,取 \(d_f=d_{fc}\)。\(d_f\) 的值介于 0~1 之间,0 代表材料完好,1 代表彻底失效。同理,可以得到 \(d_m\) 的值。
另外,无论纤维和基体发生拉伸还是压缩损伤,材料均失去承受剪切载荷的能力,因此剪切损伤变量 \(d_s\) 并非独立的损伤状态变量,\(d_s\) 取决于独立损伤状态变量 \(d_{ft}\), \(d_{fc}\), \(d_{mt}\), \(d_{mc}\),只要四个损伤状态中有一个不为 0,\(d_s\) 则不为 0,四个状态变量有一个达到 1,\(d_s\) 必然为 1。
3.5 独立损伤状态变量的求解
帮助文档以及其他能查到的资料中都给出了下列损伤状态变量 d 的统一表达式和原理图。
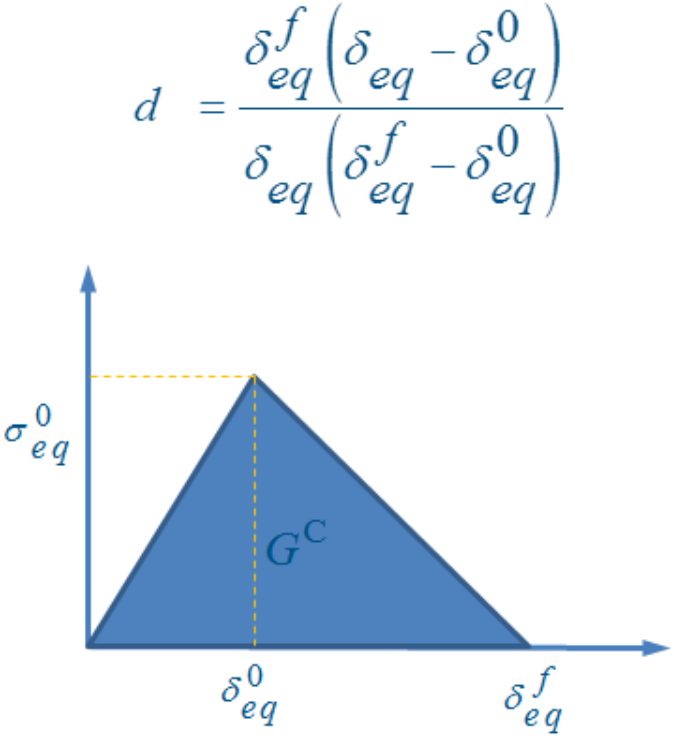
d 即为独立的损伤状态变量,要想理解损伤状态计算公式,首先需要引入两个变量定义,

那么,

注意上标 0 以及红框中标记的限定词“刚好达到 1 时”,这是理论上的数值,即某一种判据恰好判断因子等于 1 的一瞬间所记录下的等效位移,记为 \(\delta_{eq}^0\)。
该变量代表的是某个材料点某种失效模式下的损伤起始位移,对应的是上图三角形顶点的横坐标。该损伤起始位移并非一个恒定不变的材料常数,而是随着材料点的应力状态而变化的,不同的单元有可能得到不同的损伤起始位移值。这一点也是很多人不解的地方。在自己写子程序的时候,正确理解这一点很重要。
类似地,当某种失效判据判断因子恰好达到 1 时,记录下该时刻的等效应力,该等效应力即为当前材料点在当前应力状态下,某种失效模式所对应的等效强度,也就是上图中三角形顶点对应的纵坐标。同样,等效强度也不是恒定不变的材料常数。

具体到不同失效模式下,等效位移和等效应力的表达式也是有所不同的,在 Abaqus 中,纤维拉伸、纤维压缩、基体拉伸、基体压缩状态下四种等效位移和等效应力的表达式如下:
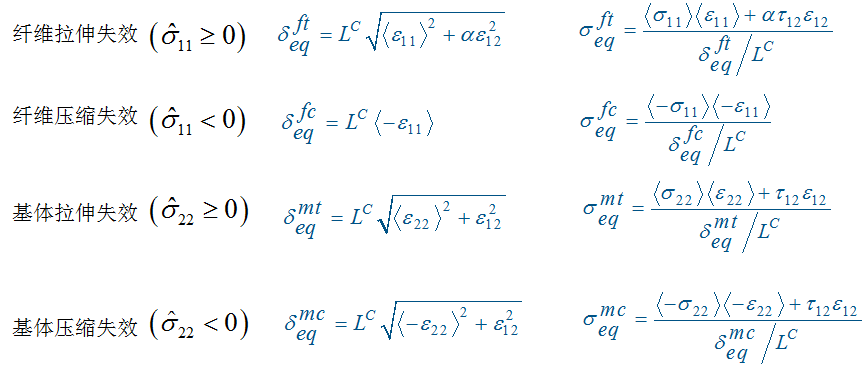
其中,\(L^C\) 为单元的特征长度,一阶面单元中特征长度是面积的平方根,一阶体单元中,特征长度是体积的立方根。
根据上述公式,再加上四种失效判据的公式,随着载荷的不断增加,就可以得到每个材料点每一种失效模式下的损伤起始位移和等效强度,损伤起始位移表达式如下:
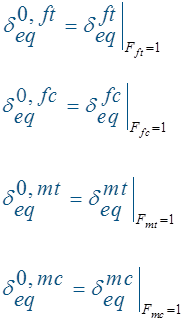
等效强度表达式如下:
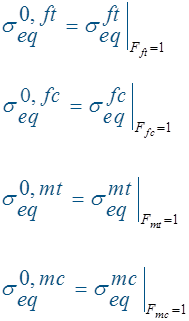
至此,每种失效模式下,损伤演化部分的损伤起始位移和等效强度就求解出来了,也就是本构三角形顶点对应的横坐标和纵坐标已知了。未知的是三角形底边的长,对应的也就是每个材料点上彻底失效时的位移。
每种失效模式彻底失效时对应的失效位移计算公式很简单:
\[\delta_{e q}^{f}=\frac{2 G^{\mathrm{C}}}{\sigma_{e q}^{0}}\]
其中 \(G^C\) 为临界应变能释放率,也就是在 CAE 中输入的损伤演化部分的断裂能(前面提到的 \(G_{ftc}\),\(G_{fcc}\),\(G_{mtc}\),\(G_{mcc}\)),也是三角形的面积。底边的长度即为两倍三角形的面积除以三角形的高,高就是等效强度,已在上一步求解得出。此时三角形中的各参数都已经可以求解出,就可以带入独立损伤状态变量 d 的计算公式了。
以纤维拉伸失效为例,
\[\delta_{e q}^{f, f t}=\frac{2 G_{f t}^{C}}{\sigma_{e q}^{0, f t}}\]
\[d_{f t}=\frac{\delta_{e q}^{f, f t}\left(\delta_{e q}-\delta_{e q}^{0, f t}\right)}{\delta_{e q}\left(\delta_{e q}^{f, f t}-\delta_{e q}^{0, f t}\right)}\]
同样的方式,四种独立的损伤状态变量就都可以求解出来了。
四种独立的损伤状态变量对应的断裂能在#3.3节中输入。
文中多次提到失效判据判断因子恰好等于的一刻,这仅仅是理论解,在实际的程序计算中,几乎不可能使判断因子恰好等于 1,有可能大于1,这种情况在自己写子程序时也是必须要考虑的。